√100以上 単項式 多項式 違い 290608-単項式 多項式 違い
「単項式」は、定数と変数(どちらも複数可)の積です。 例えば、(√3)xy^2 を単項式と呼ぶのは、この式を √3 と x と y と y との積と考えることができるからで、 √3 のカタマリを定数と見ているのです。 このような解釈が可能なら、単項式と呼びます。
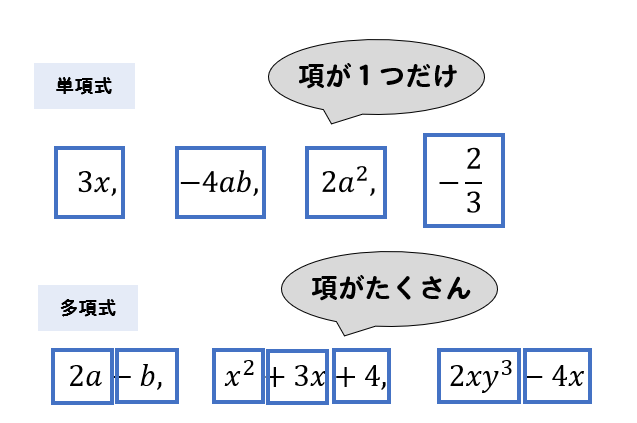
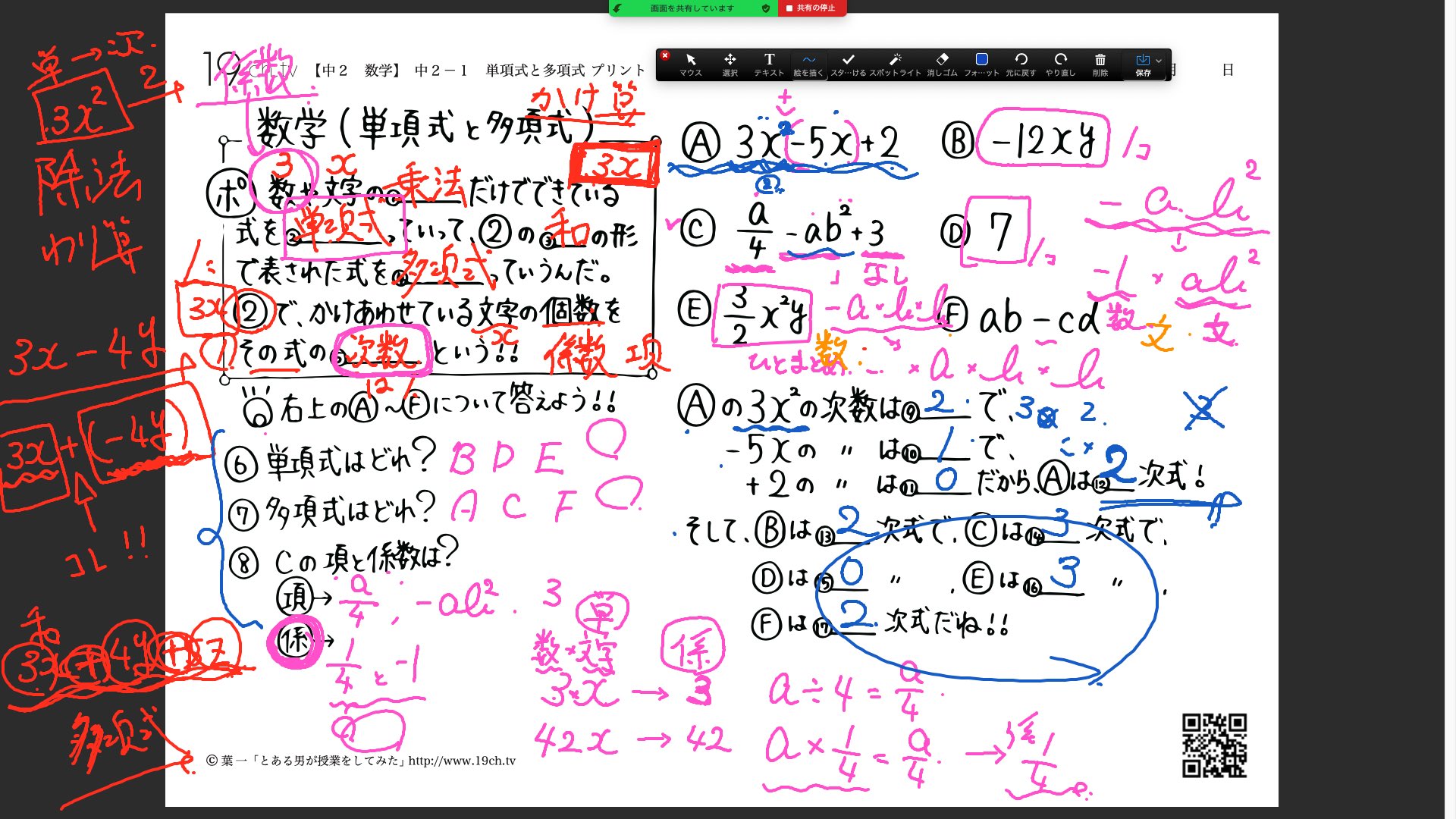
単項式 多項式 違い-多項式 単項式の複数(2つ以上)の和として表される式のこと。 例 x 3 x3 x 3 , x 2 y 2 z 2 x^2y^2z^2 x 2 y 2 z 2 , 1 x x 2 x 3 1xx^2x^3 1 x x 2 x 3 整式 単項式と多項式を合わせて整式と言います。 高校生はここまで理解すればOKです。単項式と多項式について学ぼう! 2年 1章 式の計算2/7 教P1718( )年( )組( )名前 2つの式をたしたりひいたりするには,それぞれの式にかっこをつけて,記号+,-で
単項式 多項式 違いのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  | |
 |  |  |
「単項式 多項式 違い」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「単項式 多項式 違い」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「単項式 多項式 違い」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  | |
「単項式 多項式 違い」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  |  |
「単項式 多項式 違い」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  | |
「単項式 多項式 違い」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  | |
「単項式 多項式 違い」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  |  |
「単項式 多項式 違い」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |
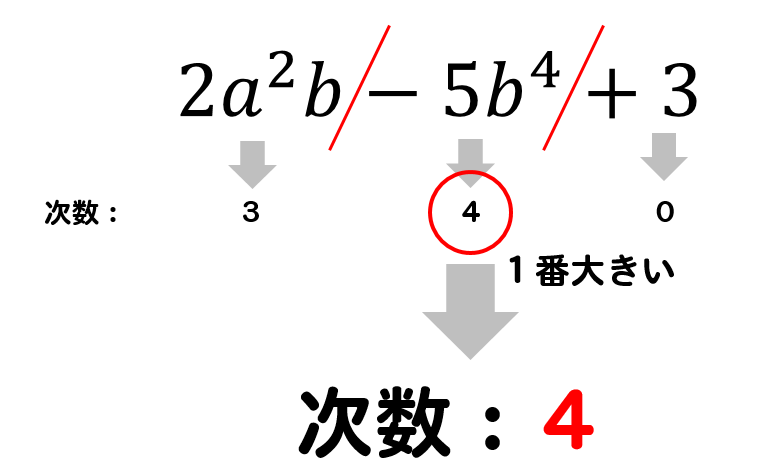
単項式,多項式,整 式の違いはどうでしょうか。 A.3x 2y のように,数と文字のかけ算で表される 式を単項式といい,単項式の和で表される式, 例えば x35xy2, を多項式という,というのが 定義ですね。単項式と多項式を合わせて多項式 そして、次数が2である式を2次式、次数が3である式を3次式といいます。 ⇒ 単項式と多項式の違いは?「単」と「多」の違いを理解すれば簡単だ! 単項式の次数、何次式
Incoming Term: 単項式 多項式 違い,
コメント
コメントを投稿